Anarkia333data.center
La Nouvelle Alexandrie Métaphysique
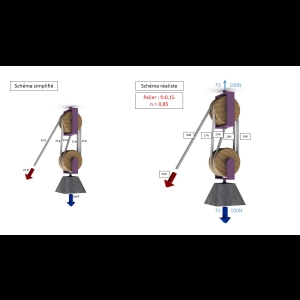
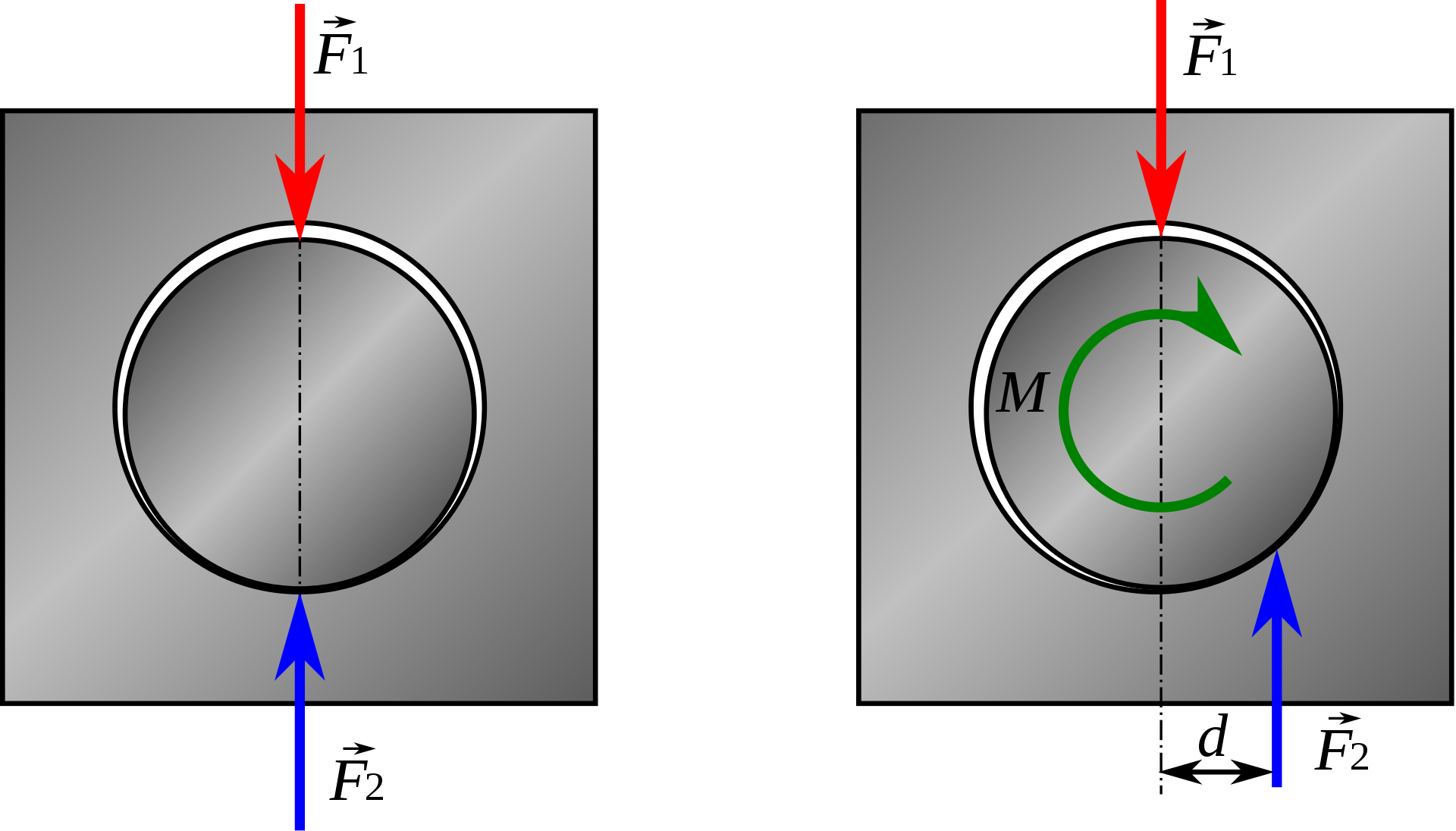
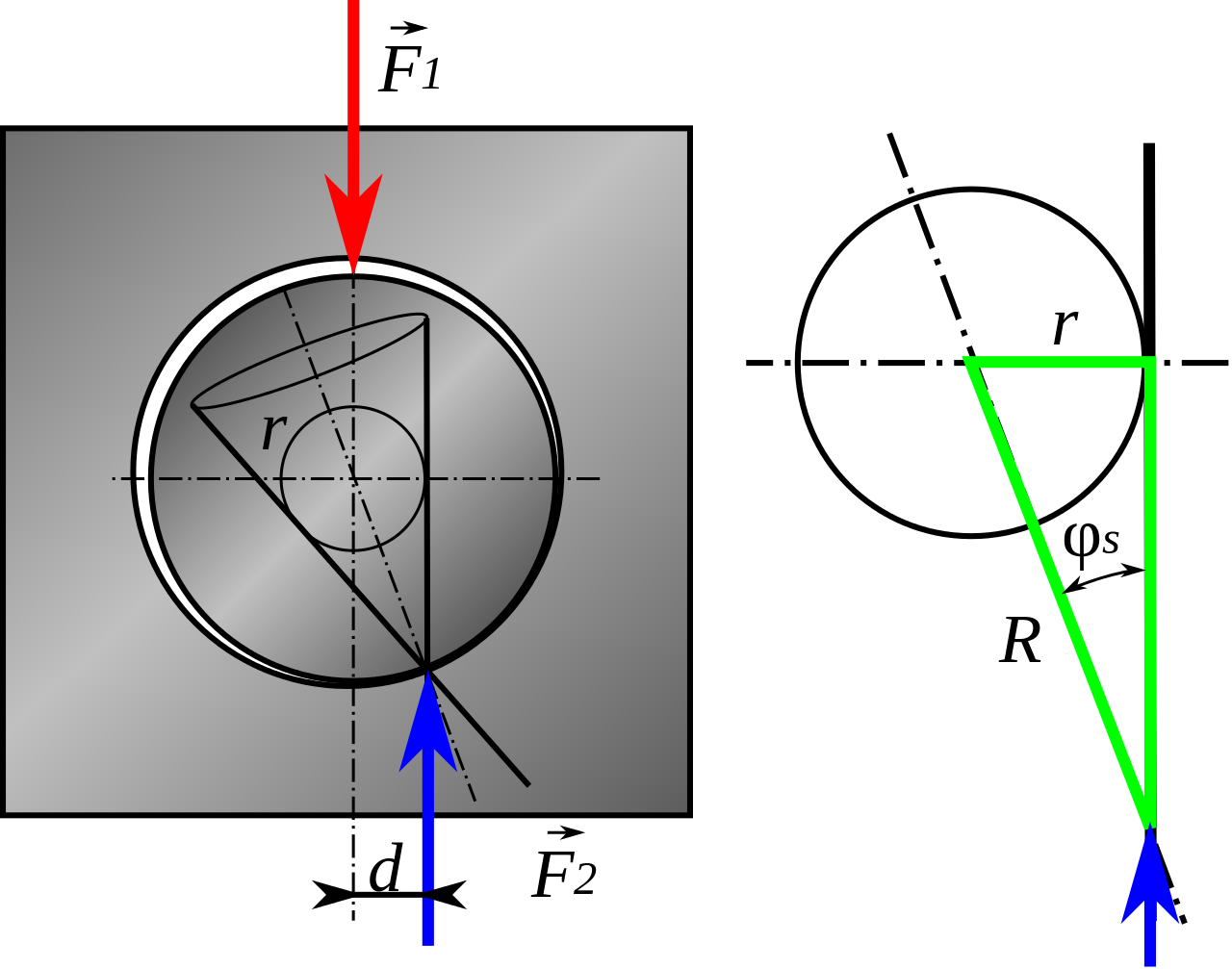
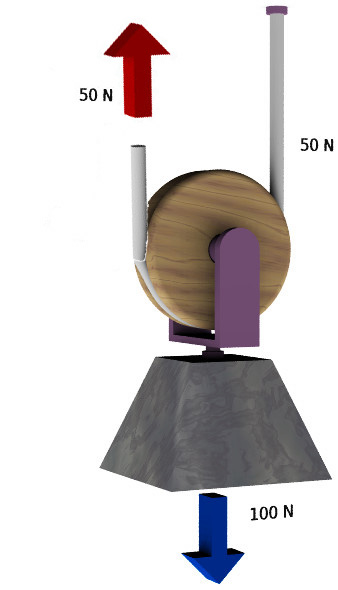
Palans/Poulies - Frottements
Menu - Mégalithes
- (Mégalithes et Anomalies) [12]
- (Mégalithes et Calculs) [15]
- (Mégalithes et Représentations) [10] Expand Secondary Navigation Menu
-
(Mégalithe et Techniques) [121]
Expand Secondary Navigation Menu
- Autres (Mégalithe et Techniques) [0]
- Abattage par le Feu [2]
- Abrasion - Blocs [0]
- Abrasion - Machines [4]
- Abrasion - Outils [13]
- Abrasion - Scie/Strie [1]
- Abrasion - Trou/Strie [6]
- Abrasion - Sarcophages [0]
- Abrasion - Vases [0]
- Cabestan [1]
- Carrières [1]
- Coeff. de Résistance [5]
- Coeff. de Sécurité [1]
- Corde - Câble [4]
- Dureté [6]
- Etat de Surface [0]
- Moulage [2]
- Levage [1]
- Maladie [1]
- Martelage [2]
- Masse [1]
- Mortoise [1]
- Outils [12]
- Poulie [3]
- Rondins et RDM [12]
- Tolérances générales [2]
- TOP Mégalithes [1]
- Traction - Animal [4]
- Traction - Humaine [3]
- Transport - Essaie réel [6]
- Transport - Techniques [7]
- Séisme [2]
- (Mégalithe et Métaphysique) [0]
- (Mégalithe : Théories) [8]
- (Prouesse Antique) [4]
- (Taille et Exp.) [20]
- Australie [1]
- Bolivie [2]
- Cambodge [0]
- Chine [0]
- Corse [0]
- Egypte [13]
- Espagne [0]
- Éthiopie [5]
- France [0]
- Grèce [0]
- Île de Pâques [0]
- Inde [10] Expand Secondary Navigation Menu
- Iran [1]
- Italie [2]
- Japon [0]
- Malte [0]
- Mexique [0]
- Pérou [10]
- Proche-Orient [14] Expand Secondary Navigation Menu
- Russie [0]
- Sardaigne [0]
- Turquie [0]
- Uk [4]
Copyright All Rights Reserved
Developed & Designed by Alaa Haddad