En mécanique classique, on calcule la résistance du matériaux par rapport à sa limite élastique, puis appliquons un coefficient de sécurité.
Si la limité élastique est dépassé, la matière entre en déformation plastique : elle reste déformé. Ce qu'on évite absolument en mécanique classique.
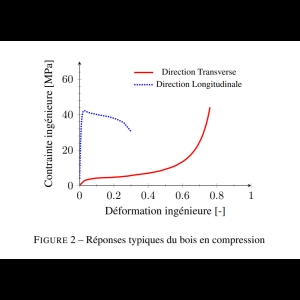
En compression Radial (perpendiculaire aux fibres) le bois se situe entre 4-8 Mpa en moyenne pour son Re (limite élastique), ce qui est très faible en résistance. (Un Acier se situe autour de 250-300Mpa minimum).
- Valeur Max retenue en comrpession Radial pour le Bois en déformation plastique
Pression Théorique possible admissible : 10 fois sa résistance élastique en Radial pour 70% de déformation
Les 1ers calculs démontre que cette valeur est largement dépassé, exemple avec le Monolithe Mussolini - 300T :
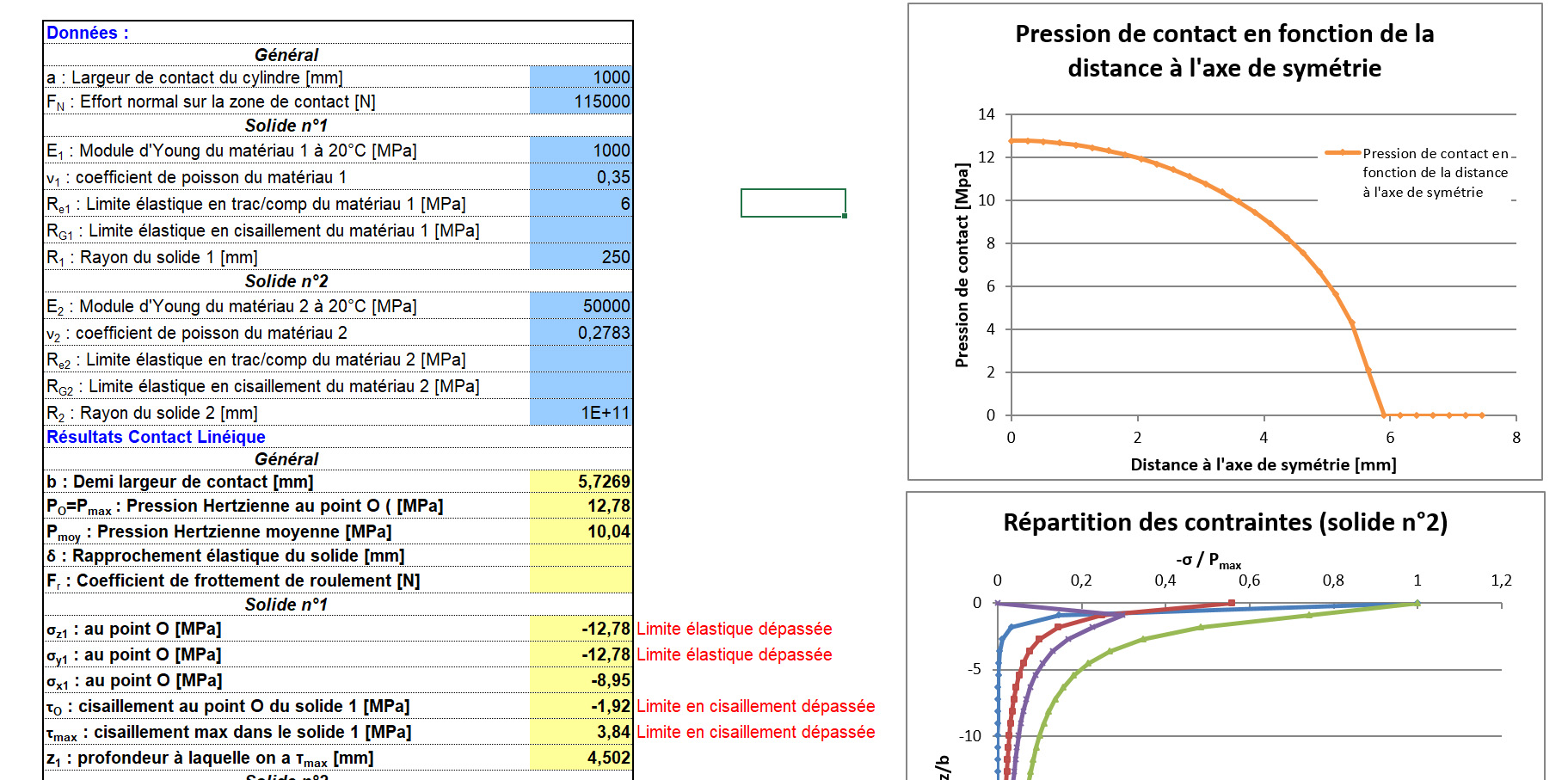
(Contact de Hertz : Cylindre/Plan)
Sachant que ce calcul se base sur un appuie parfait des rondins, dans la réalité et sous conditions défavorable (Pente,...) les rondins prendront 2 à 3 fois plus d'effort soit 35-40Mpa.
Les formules classiques dans le domaine élastique ne fonctionne plus. Le bois est en régime plastique. Le Bois se déforme et donc la pression se répartie d'avantage.
Limite Plastique Ultime du Bois
Il peut être donc nécessaire de connaître la valeur de résistance ultime ou limite (Ultimate stress).
Mais cette valeur échappe aux test de laboratoire, voici ce qu'on peut lire ici :
Compressive stress perpendicular to grain—Reported as stress at proportional limit. There is no clearly defined ultimate stress for this property.
(Mechanical Properties of Wood)
Exemple de déformation plastique du Bois :
Tin déformé par le Poids du navire:

Rondins déformé par le Poids du Monolithe de Mussolini:

Module de Young d'élasticité du Bois en Radial
Le module de Young du Bois en Radial est d'environ 1000Mpa. Voir Bois : Module E Radiale et Coeff. de Poisson.
Erreur classique
Nombreuses théorie ont été émise sur l'impossibilité de charge du Bois sous de forte pression, mais les Tests Réels comme le Monolithe Mussolini - 300T démontre l'inverse, car le bois entre en déformation plastique. Le calcul se montre dans ce cas précis plus complexe.
Coefficient de sécurité
Valeurs de Tests Réels
Voir Transport : Monolithe Mussolini - 300T.
Sachant que le Monolithe de Mussolini à une masse de 300T, si on divise par 26 (Nombres de rondins de bois en appuie Radial), on obtient 11.5T par rondins, sachant qu'en certaines conditions défavorable certains rondins prendrons plus de charge (Descente, sol non plat, ...), nous rajoutons un Cs de 3. Les Vidéos ne montrant aucune casse, on peut en déduire que la marge du Cs est encore large.
Donc un rondins de bois basique (Cerisier ; Re=4.8Mpa en Radial) peut tenir 34.5T au minimum en déformation plastique, avec une surface d'appuie de 1500mm.
Valeurs de Laboratoire en comportement Elastique non-linéaire
Voir Bois : Comportement Elastique non-linéaire
Ce test très intéressante montre que bois en compression Radial peut supporter 10 fois sa résistance élastique. Et sa forte déformation permet de répartir les contraintes de pression.
Nous pouvons émettre l'hypothèse que le bois peut supporter 40 Mpa pour du Bois de 4Mpa pour une déformation de 70%.
Un Bois à la résistance double pourrait donc supporté 80Mpa pour une déformation de 70%.
Calcul Théorique de charge Maximum pour un Rondins de Bois
Si on prend un Rondins de Bois avec une résistance élastique de 4Mpa (Bois basique), écraser de 70%, d'une longueur de 2m. Et que l'on considère que la technique de la Luge est utilisé pour les fortes charges. Alors la surface de contact Totale est de 382 000mm².
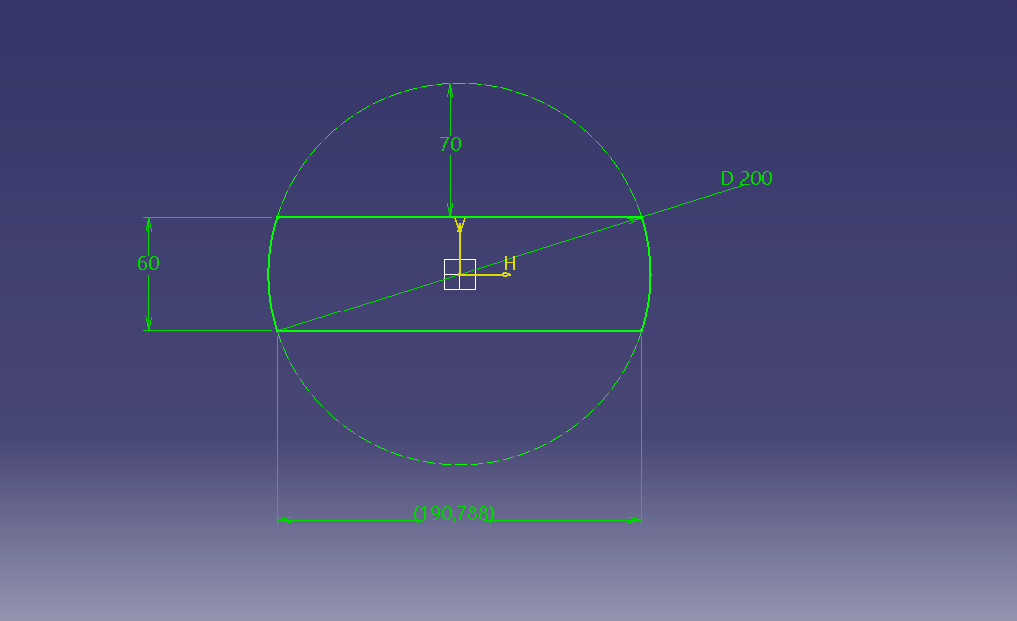

Si on considère que le contact Luge/Rondins se fait sur 1m, on obtient une surface de contact de 191 000mm².
En appliquant P=F/S soit P*S=F :
F = 40 * 191 000 = 7 640 000 Newton, soit 780 Tonnes pour du Bois de 4Mpa en Radial.
SI on applique un Coeff. de sécurité de 3, et que l'on multiplie par 26, on obtient 6700T.
26 Rondins de Bois pourrait donc en Théorie supporté 6700T avec un Cs de 3, avec la technique de la Luge par glissement.
Modèle en Elément Finie non-linéaire
Des Logiciels existe pour calculer la résistance des Matériaux, ils sont utilisé en Génie Mécanique dans de nombreux domaines : Aéronautique, Automobile, Structure....
Le régime du Bois étant dans le domaine plastique, il est donc nécessaire d'utilisé un Logiciel d'élément Finie non-linéaire comme Abaqus : Logiciel : "Abaqus/SIMULIA"
(Etude en cours)
Conclusion
Le Bois est un un matériaux formidable pour la compression, et ne semble presque pas avoir de limite. Nous émettons l'hypothèse qu'un Rondins de bois basique (Re=4Mpa en Radial) peut supporter 780T (sans Cs), la Pierre de Baalbek de 1000T pourrait donc avoir été transportez par seulement 4 Rondins (Cs de 3) de façon purement théorique sans tenir conte de technique et praticité.
Un Rondins 3 fois supérieur de 12 Mpa en Radial pourrait donc supporté 2340T.
Nous en concluons que le Bois n'est pas une limite à la réalisation du transport de Mégalithes.