Trop souvent considéré comme un élément perturbateur pour les calculs, on s’aperçoit très vite que le frottement est tout simplement indispensable : si les vis de fixation restent serrées, le clou en place, les échelles debout et les voitures sur la route, c’est grâce au frottement. C’est aussi sur ce phénomène que repose le fonctionnement des freins et embrayages.
Pour résoudre un problème de statique, sa considération systématique n’est pas obligatoire. Il existe des modèles mathématiques simples, et cependant précis qui décrivent ce phénomène. Les lois de Coulomb font partie de ces modèles. La tribologie est la science du contact qui propose d'autres modèles plus pointus à utiliser suivant les exigences de l'étude.
(Source: Wikipédia ; sous Licence CC BY-SA 3.0)
Valeur Retenue pour les Coeffs. de frottement pour le Bois:
Statique : 0.040
Dynamique : 0.027
- Coeff. de frottements : Arthur Morin
Materials and Material Combinations Surface Conditions Frictional Coefficient Static
- μstatic -Sliding
- μsliding -Wood Clean Wood Clean and Dry 0.25 - 0.5 Wood Wet Wood Clean and Dry 0.2 Wood Stone Clean and Dry 0.2-0.4
(Source : Engineering ToolBox)Materials Static friction Sliding friction Dry Greasy Dry Greasy Oak on Oak (parallel to grain) 0.62 0.48 0.164 (Dry soap) ; 0.067 (Lard) Oak on Oak (perpendicular) 0.54 0.32 0.072 (Lard) Oak on Oak wet (perpendicular) 0.71 0.25
(Source : Theory and Practice of Lubrication for Engineers (Baser sur Arthur Morin))Matériaux (Fibres/Sens) Statique Dynamique Sec Lubrifié Sec Lubrifié Chêne sur chêne (parallèles) 0.60-0.65 0.44 (a) 0.48 0.16 (a) Chêne sur chêne (perpendiculaire) 0.54 0.32 Chêne sur chêne (perpendiculaire/mouillé) 0.71 0.25 Chêne sur orme (parallèles) 0.38 Orme sur chêne (parallèles) 0.69 0.41 (a) 0.43 Orme sur chêne (perpendiculaire) 0.57 0.45 Frêne sur chêne (parallèles) 0.50 0.40 Sapin sur chêne (parallèles) 0.52 0.36 Hêtre sur chêne (parallèles) 0.53 0.36 Poirier sauvage sur chêne (parallèles) 0.44 0.40 Sorbier sur chêne (parallèles) 0.57 Chêne, orme, fonte, bronze, fer, charme l'un sur l'autre (à plat) 0.10 (b), 0.15 (c) Chêne, orme, charme, poirier sauvage, fonte, fer, acier et bronze glissant l'un sur l'autre ou sur eux-mêmes (parallèles) 0.08 (b;c), 0.15 (d), 0.04 (e) a: frotté au savon sec
b: enduites de suif
c: enduites d'huile ou de saindoux
d: légèrement onctueuses au toucher
e: si l'enduit est renouvelé sans cesse et uniformément répartie(Source : Arthur Morin)
Coeff. de frottement sur sable mouillé : 0.30, voir étude Sliding Friction on Wet and Dry Sand.
- Coeff. de frottements : Guide de mécanique
Les valeurs du Bois semble provenir de Arthur Morin :
- Coeff. de frottements : AIAA Aerospace Design Engineers Guide
Détails - Mégalithe
- Coefficient f de frottement : Wikipédia
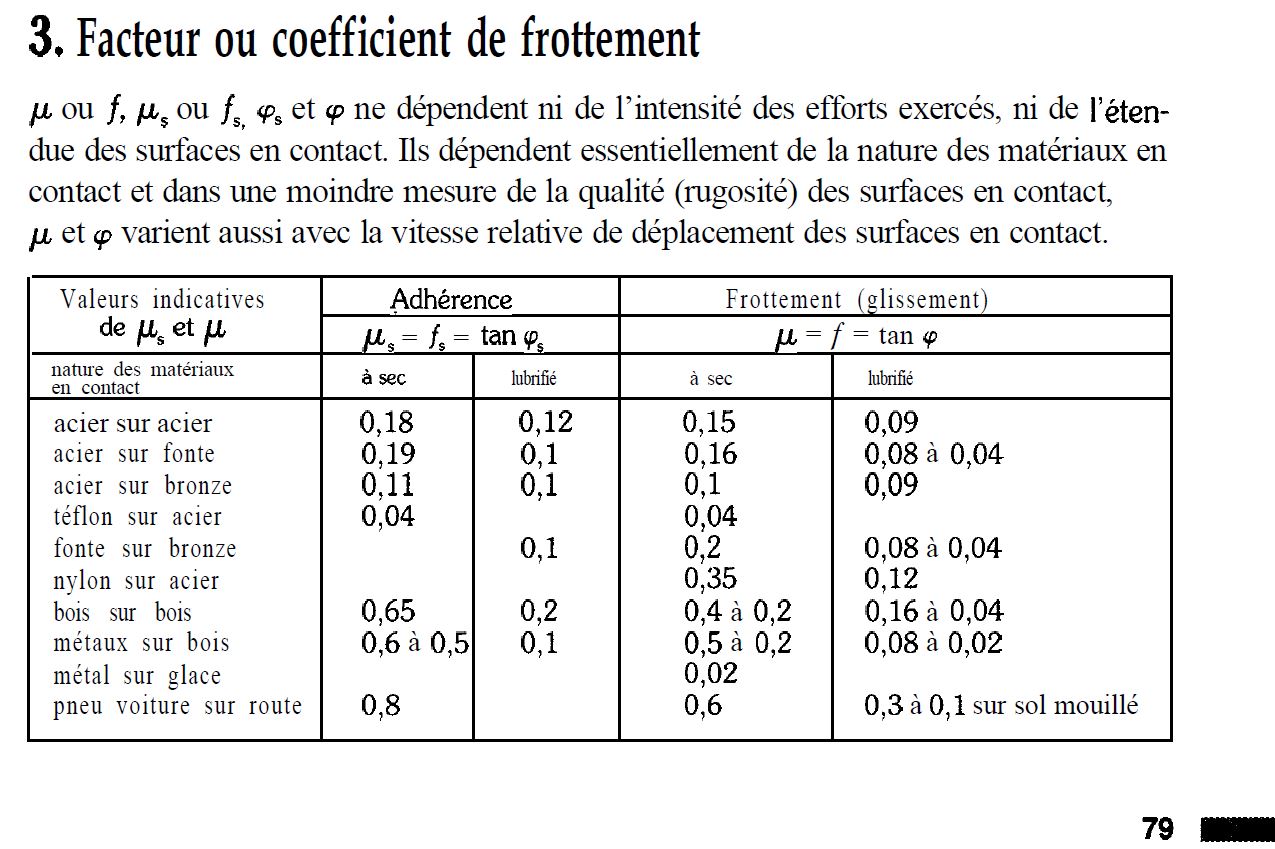
La valeur de ces coefficients n’est pas modélisable et ne peut s’établir que par la mesure. On trouvera de nombreuses valeurs directement applicables dans le wikilivre de tribologie.
Selon les lois de Coulomb, qui constituent un premier modèle simpliste mais souvent suffisant, ces valeurs ne dépendent que de la nature des matériaux mis en présence et de l'état de leurs surfaces ; elles sont indépendantes des formes des surfaces de contact, de leurs dimensions, des pressions de contact et de la vitesse de glissement. La complexité du modèle doit être adaptée au besoin. La tribologie indique l'ensemble des facteurs à considérer si un modèle trop simple ne convenait pas.
La différence entre le coefficient de frottement et le coefficient d'adhérence étant souvent faible, les deux valeurs peuvent être confondues. Voici quelques valeurs numériques pour les coefficients d’adhérence (glissement):
- Acier / acier : 0,2 (0,15)- 0.3
- Acier / glace : 0,02 (0,02)
- Acier / bronze : 0,1 (0,05)
- Acier / garnitures de freins : 0,4 (0,25) (pression maxi 20 MPa, T°<200°C)
- Pneu / route sèche : 0,8 (0,5)
- Pneu / route mouillée : 0,5 (0,35)
(Source: Wikipédia ; sous Licence CC BY-SA 3.0)
- Coefficient f de frottement : WIKIBOOKS - Tribologie/Facteurs de frottement
Définitions
Les facteurs de frottement et d'adhérence (on dit aussi coefficients de frottement et d'adhérence) sont définis dans ce chapitre du livre.
Lorsque des efforts normaux sont transmis d'un corps à un autre essentiellement par des contacts d'aspérités, les facteurs de frottement varient typiquement de un à quelques dixièmes mais il existe beaucoup d'exceptions. Certains couples de matériaux permettent en effet d'obtenir des valeurs inhabituellement faibles, de l'ordre de quelques centièmes, tandis que d'autres procurent des valeurs beaucoup plus élevées, proches de l'unité ou même supérieures à un, en particulier dans des systèmes « fermés ». Les valeurs qui figurent dans le tableau ci-dessous relèvent de ces situations.
Les efforts normaux peuvent aussi être transmis par des couches fluides mises sous pression et cisaillées lors du mouvement. Toute adhérence disparaît alors et les valeurs du coefficient de frottement ne dépendent plus de la nature des matériaux en présence mais d'autres paramètres comme la vitesse, la pression, la viscosité et l'épaisseur de la couche fluide. Les valeurs varient alors de quelques millièmes à l'infini, puisque la déformation du fluide peut engendrer des efforts tangentiels sans que le moindre effort normal soit transmis. Ces coefficients de frottement n'ont pas leur place dans ce chapitre, leur étude relève de la technologie des guidages lisses.
Il en va de même pour les coefficients de frottement de roulement qui, rappelons-le, sont des longueurs.
Gamme de variation
Le facteur de frottement est une grandeur qui varie très fortement en fonction de très nombreux paramètres : état de surface et lubrification évidemment, mais aussi vitesse, pression, temps de maintien en charge, etc. On relève les ordres de grandeur suivants :
plus de 1 pour des surfaces dégazées dans le vide, avec parfois soudure immédiate 0,3 à 1 pour le frottement de deux métaux non préparés dans l'air, à sec 0,1 à 0,2 pour la plupart des métaux dans l'air avec les lubrifiants usuels (huile) dans le cas de la lubrification onctueuse 0,05 à 0,1 pour des surfaces préparées convenablement, lubrifiées avec du graphite, du bisulfure de molybdène ou certains acides gras 0,02 à 0,05 pour le frottement sur la glace, pour le PTFE sur lui-même sous charge suffisante à faible vitesse 0,01 à 0,001 pour les paliers lisses en régime hydrodynamique bien calculés, en l'absence de tout contact solide (par exemple, dans les anciens essieux de wagons) 0,0001 ou moins pour les guidages hydrostatiques ou aérostatiques 0,00001 ou moins encore pour les paliers magnétiques actifs Dans ces deux derniers cas, le bilan énergétique global doit toutefois tenir compte de la puissance nécessaire à l'alimentation du palier en fluide sous pression ou en électricité
Valeurs numériques indicatives.Les valeurs qui suivent sont des ordres de grandeur donnés à titre purement indicatif. Du reste dans les documentations techniques on trouve souvent des données très divergentes.
couple de matériaux facteur d'adhérence facteur de frottement à sec limite onctueux à sec limite onctueux acier doux sur acier doux (air sec) 1,2 1,2 acier doux (vapeur d'eau) 1,2 à sec limite onctueux à sec limite onctueux acier mi-dur sur acier mi-dur 0,3 0,2 0,17 0,11 acier trempé 0,2 0,17 0,14 0,17 0,15 0,1 acier, boulonnerie 0,28 à 0,43 acier, frettage par pression d'huile 0,12 acier, frettage par pression de glycérine 0,18 acier, frettage à chaud 0,14 id., surfaces dégraissées 0,2 alliages de WOOD 0,7 0,1 aluminium (alliages) 0,16 0,12 0,08 antifriction base étain 0,25 0,8 0,20 0,11 antifriction base plomb 0,25 0,55 0,10 à 0,08 bisulfure de molybdène 70 MPa 0,07 350 MPa 0,05 1 400 MPa 0,045 2 800 MPa 0,023 Le facteur de frottement est moins élevé en ambiance sèche
Dans les huiles de viscosité moyenne, 1 % de bisulfure de molybdène peut diviser f par 2acier mi-dur (suite) sur bronze 0,35 0,18 0,1 0,3 0,1 0,08 caoutchouc 1 à 4 carbure de tungstène 0,5 0,15 chlorure de polyvinyle 0,5 cuir 0,18 à 0,35 0,12 à 0,18 cupro-plomb 0,2 0,2 0,12 0,08 fonte 0,4 0,18 0,1 0,4 0,05 à 0,1 graphite 0,1 indium en film mince 0,08 nickel (aboutit au grippage) 0,6 à 0,8 nylon 0,3 polyméthacrylate de méthyle 0,45 polystyrène 0,5 P.T.F.E. 0,05 à sec limite onctueux à sec limite onctueux acier inoxydable sur alliage léger traité Zinal 0,2 aluminium sur aluminium (air sec) 1,9 aluminium (vapeur d'eau) 1,1 antifriction sur antifriction 0,54 0,19 bois sur métal 0,6 à 0,7 0,12 0,4 à 0,5 0,1 bronze sur bronze 0,2 fonte 0,21 carbure de tungstène sur lui-même, propre 0,2 chrome dur sur acier 0,17 0,16 antifriction 0,15 0,13 chrome 0,14 0,12 Le chrome diminue le pouvoir mouillant des huiles par rapport à l'acier.
Il est utilisable avec une lubrification à l'eau en face du cuir, des plastiques et des élastomères.à sec limite onctueux à sec limite onctueux courroies caoutchouc sur fonte 0,4 à 0,5 textile sur fonte 0,3 à 0,5 fer sur fer 0,4 fonte sur cuir 0,18 à 0,35 0,12 à 0,18 fonte 1,2 0,16 0,14 0,12 0,05 à 0,1 P.T.F.E. voir acier garnitures de freins
ou d'embrayages suracier 0,25 à 0,35 glace ou neige sur glace ou métaux jusqu'à -30°C 0,02 à 0,03 Le coefficient très bas est attribué à la fusion provoquée par le frottement.
Ce dernier est en revanche très difficile en-dessous de - 30 à - 40 °C, le coefficient atteint alors 0,4.
On explique ainsi des accidents d'avion montés sur skis atterrissant sur la banquise.à sec limite onctueux à sec limite onctueux graphite sur graphite 0,2 Nylon sur nylon 0,5 0,5 caoutchouc sur verre sec jusqu'à 2 pneumatiques sur chaussée sèche 0,6 à 0,8 chaussée mouillée (hors aquaplaning) 0,3 à 0,4 saphir ou rubis sur saphir 0,2 acier 0,15 si nettoyage sous vide 0,6 roues Le frottement de roulement s'exprime par un moment M proportionnel à la charge N
supportée par la roue et à une distance d qui constitue le coefficient de frottement de roulement.
M = d x N, avec d de 6 à 8 mm pour des roues d'automobiles, 1 à 2 mm pour une roue de wagon, 0,497 mm pour les pneus Michelin utilisés à l'éco-marathon Shell.
(Source: Wikibooks ; sous Licence CC BY-SA 3.0)- Coefficient f de frottement : Engineering ToolBox
Friction Coefficients for some Common Materials and Materials Combinations
Materials and Material Combinations Surface Conditions Frictional Coefficient Static
- μstatic -Sliding
- μsliding -Aluminum Aluminum Clean and Dry 1.05 - 1.35 1.4 Aluminum Aluminum Lubricated and Greasy 0.3 Aluminum-bronze Steel Clean and Dry 0.45 Aluminum Mild Steel Clean and Dry 0.61 0.47 Aluminum Snow Wet 0oC 0.4 Aluminum Snow Dry 0oC 0.35 Brake material2) Cast iron Clean and Dry 0.4 Brake material2) Cast iron (wet) Clean and Dry 0.2 Brass Steel Clean and Dry 0.51 0.44 Brass Steel Lubricated and Greasy 0.19 Brass Steel Castor oil 0.11 Brass Cast Iron Clean and Dry 0.3 Brass Ice Clean 0oC 0.02 Brass Ice Clean -80oC 0.15 Brick Wood Clean and Dry 0.6 Bronze Steel Lubricated and Greasy 0.16 Bronze Cast Iron Clean and Dry 0.22 Bronze - sintered Steel Lubricated and Greasy 0.13 Cadmium Cadmium Clean and Dry 0.5 Cadmium Cadmium Lubricated and Greasy 0.05 Cadmium Chromium Clean and Dry 0.41 Cadmium Chromium Lubricated and Greasy 0.34 Cadmium Mild Steel Clean and Dry 0.46 Cast Iron Cast Iron Clean and Dry 1.1 0.15 Cast Iron Cast Iron Clean and Dry 0.15 Cast Iron Cast Iron Lubricated and Greasy 0.07 Cast Iron Oak Clean and Dry 0.49 Cast Iron Oak Lubricated and Greasy 0.075 Cast iron Mild Steel Clean and Dry 0.4 Cast iron Mild Steel Clean and Dry 0.23 Cast iron Mild Steel Lubricated and Greasy 0.21 0.133 Car tire Asphalt Clean and Dry 0.72 Car tire Grass Clean and Dry 0.35 Carbon (hard) Carbon Clean and Dry 0.16 Carbon (hard) Carbon Lubricated and Greasy 0.12 - 0.14 Carbon Steel Clean and Dry 0.14 Carbon Steel Lubricated and Greasy 0.11 - 0.14 Chromium Chromium Clean and Dry 0.41 Chromium Chromium Lubricated and Greasy 0.34 Copper-Lead alloy Steel Clean and Dry 0.22 Copper Copper Clean and Dry 1.6 Copper Copper Lubricated and Greasy 0.08 Copper Cast Iron Clean and Dry 1.05 0.29 Copper Mild Steel Clean and Dry 0.53 0.36 Copper Mild Steel Lubricated and Greasy 0.18 Copper Mild Steel Oleic acid 0.18 Copper Glass Clean and Dry 0.68 0.53 Cotton Cotton Threads 0.3 Diamond Diamond Clean and Dry 0.1 Diamond Diamond Lubricated and Greasy 0.05 - 0.1 Diamond Metals Clean and Dry 0.1 - 0.15 Diamond Metal Lubricated and Greasy 0.1 Garnet Steel Clean and Dry 0.39 Glass Glass Clean and Dry 0.9 - 1.0 0.4 Glass Glass Lubricated and Greasy 0.1 - 0.6 0.09 - 0.12 Glass Metal Clean and Dry 0.5 - 0.7 Glass Metal Lubricated and Greasy 0.2 - 0.3 Glass Nickel Clean and Dry 0.78 Glass Nickel Lubricated and Greasy 0.56 Graphite Steel Clean and Dry 0.1 Graphite Steel Lubricated and Greasy 0.1 Graphite Graphite (in vacuum) Clean and Dry 0.5 - 0.8 Graphite Graphite Clean and Dry 0.1 Graphite Graphite Lubricated and Greasy 0.1 Hemp rope Timber Clean and Dry 0.5 Horseshoe Rubber Clean and Dry 0.68 Horseshoe Concrete Clean and Dry 0.58 Ice Ice Clean 0oC 0.1 0.02 Ice Ice Clean -12oC 0.3 0.035 Ice Ice Clean -80oC 0.5 0.09 Ice Wood Clean and Dry 0.05 Ice Steel Clean and Dry 0.03 Iron Iron Clean and Dry 1.0 Iron Iron Lubricated and Greasy 0.15 - 0.20 Lead Cast Iron Clean and Dry 0.43 Leather Oak Parallel to grain 0.61 0.52 Leather Metal Clean and Dry 0.4 Leather Metal Lubricated and Greasy 0.2 Leather Wood Clean and Dry 0.3 - 0.4 Leather Clean Metal Clean and Dry 0.6 Leather Cast Iron Clean and Dry 0.6 0.56 Leather fiber Cast iron Clean and Dry 0.31 Leather fiber Aluminum Clean and Dry 0.30 Magnesium Magnesium Clean and Dry 0.6 Magnesium Magnesium Lubricated and Greasy 0.08 Magnesium Steel Clean and Dry 0.42 Magnesium Cast Iron Clean and Dry 0.25 Masonry Brick Clean and Dry 0.6 - 0.7 Mica Mica Freshly cleaved 1.0 Nickel Nickel Clean and Dry 0.7 - 1.1 0.53 Nickel Nickel Lubricated and Greasy 0.28 0.12 Nickel Mild Steel Clean and Dry 0.64 Nickel Mild Steel Lubricated and Greasy 0.178 Nylon Nylon Clean and Dry 0.15 - 0.25 Nylon Steel Clean and Dry 0.4 Nylon Snow Wet 0oC 0.4 Nylon Snow Dry -10oC 0.3 Oak Oak (parallel grain) Clean and Dry 0.62 0.48 Oak Oak (cross grain) Clean and Dry 0.54 0.32 Oak Oak (cross grain) Lubricated and Greasy 0.072 Paper Cast Iron Clean and Dry 0.20 Phosphor-bronze Steel Clean and Dry 0.35 Platinum Platinum Clean and Dry 1.2 Platinum Platinum Lubricated and Greasy 0.25 Plexiglas Plexiglas Clean and Dry 0.8 Plexiglas Plexiglas Lubricated and Greasy 0.8 Plexiglas Steel Clean and Dry 0.4 - 0.5 Plexiglas Steel Lubricated and Greasy 0.4 - 0.5 Polystyrene Polystyrene Clean and Dry 0.5 Polystyrene Polystyrene Lubricated and Greasy 0.5 Polystyrene Steel Clean and Dry 0.3 - 0.35 Polystyrene Steel Lubricated and Greasy 0.3 - 0.35 Polyethylene Polytehylene Clean and Dry 0.2 Polyethylene Steel Clean and Dry 0.2 Polyethylene Steel Lubricated and Greasy 0.2 Rubber Rubber Clean and Dry 1.16 Rubber Cardboard Clean and Dry 0.5 - 0.8 Rubber Dry Asphalt Clean and Dry 0.9 0.5 - 0.8 Rubber Wet Asphalt Clean and Dry 0.25 - 0.75 Rubber Dry Concrete Clean and Dry 0.6 - 0.85 Rubber Wet Concrete Clean and Dry 0.45 - 0.75 Silk Silk Clean 0.25 Silver Silver Clean and Dry 1.4 Silver Silver Lubricated and Greasy 0.55 Sapphire Sapphire Clean and Dry 0.2 Sapphire Sapphire Lubricated and Greasy 0.2 Silver Silver Clean and Dry 1.4 Silver Silver Lubricated and Greasy 0.55 Skin Metals Clean and Dry 0.8 - 1.0 Steel Steel Clean and Dry 0.5 - 0.8 0.42 Steel Steel Lubricated and Greasy 0.16 Steel Steel Castor oil 0.15 0.081 Steel Steel Steric Acid 0.005 0.029 Steel Steel Light mineral oil 0.23 Steel Steel Lard 0.11 0.084 Steel Steel Graphite 0.058 Steel Graphite Clean and Dry 0.21 Straw Fiber Cast Iron Clean and Dry 0.26 Straw Fiber Aluminum Clean and Dry 0.27 Tarred fiber Cast Iron Clean and Dry 0.15 Tarred fiber Aluminum Clean and Dry 0.18 Polytetrafluoroethylene (PTFE) (Teflon) Polytetrafluoroethylene (PTFE) Clean and Dry 0.04 0.04 Polytetrafluoroethylene (PTFE) Polytetrafluoroethylene (PTFE) Lubricated and Greasy 0.04 Polytetrafluoroethylene (PTFE) Steel Clean and Dry 0.05 - 0.2 Polytetrafluoroethylene (PTFE) Snow Wet 0oC 0.05 Polytetrafluoroethylene (PTFE) Snow Dry 0oC 0.02 Tungsten Carbide Steel Clean and Dry 0.4 - 0.6 Tungsten Carbide Steel Lubricated and Greasy 0.1 - 0.2 Tungsten Carbide Tungsten Carbide Clean and Dry 0.2 - 0.25 Tungsten Carbide Tungsten Carbide Lubricated and Greasy 0.12 Tungsten Carbide Copper Clean and Dry 0.35 Tungsten Carbide Iron Clean and Dry 0.8 Tin Cast Iron Clean and Dry 0.32 Tire, dry Road, dry Clean and Dry 1 Tire, wet Road, wet Clean and Dry 0.2 Wax, ski Snow Wet 0oC 0.1 Wax, ski Snow Dry 0oC 0.04 Wax, ski Snow Dry -10oC 0.2 Wood Clean Wood Clean and Dry 0.25 - 0.5 Wood Wet Wood Clean and Dry 0.2 Wood Clean Metal Clean and Dry 0.2 - 0.6 Wood Wet Metals Clean and Dry 0.2 Wood Stone Clean and Dry 0.2 - 0.4 Wood Concrete Clean and Dry 0.62 Wood Brick Clean and Dry 0.6 Wood - waxed Wet snow Clean and Dry 0.14 0.1 Wood - waxed Dry snow Clean and Dry 0.04 Zinc Cast Iron Clean and Dry 0.85 0.21 Zinc Zinc Clean and Dry 0.6 Zinc Zinc Lubricated and Greasy 0.04
(Source: https://www.engineeringtoolbox.com/)
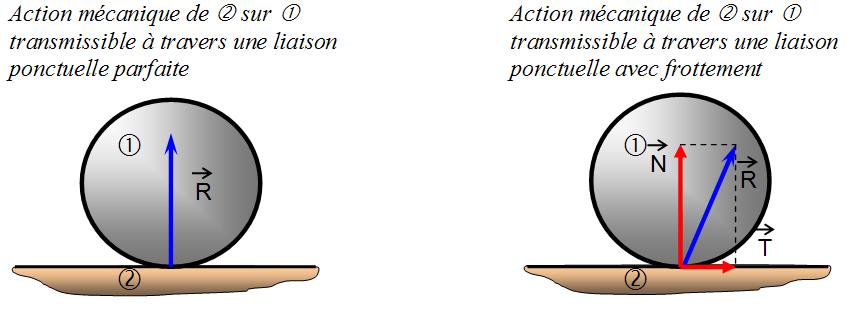
Contact parfait et contact avec frottement
Dans un contact parfait, l’action mécanique transmissible par obstacle entre 2 solides ne peut être en tout point que normale au contact (perpendiculaire au plan tangent commun du contact). Pour que cette action mécanique puisse prendre une autre direction, il y a nécessité d’une composante tangentielle qui ne sera pas transmise par obstacle mais par frottement ou adhérence.
La force résultante transmise dans ce contact se projette suivant une composante normale, dite effort presseur, et une composante tangentielle dite force de frottement.
Il n'est pas toujours nécessaire de distinguer ces composantes lors d'une étude statique (voir lois de Coulomb ci-dessous).
On a deux types de contacts : réparti et engendré.
Adhérence et glissement
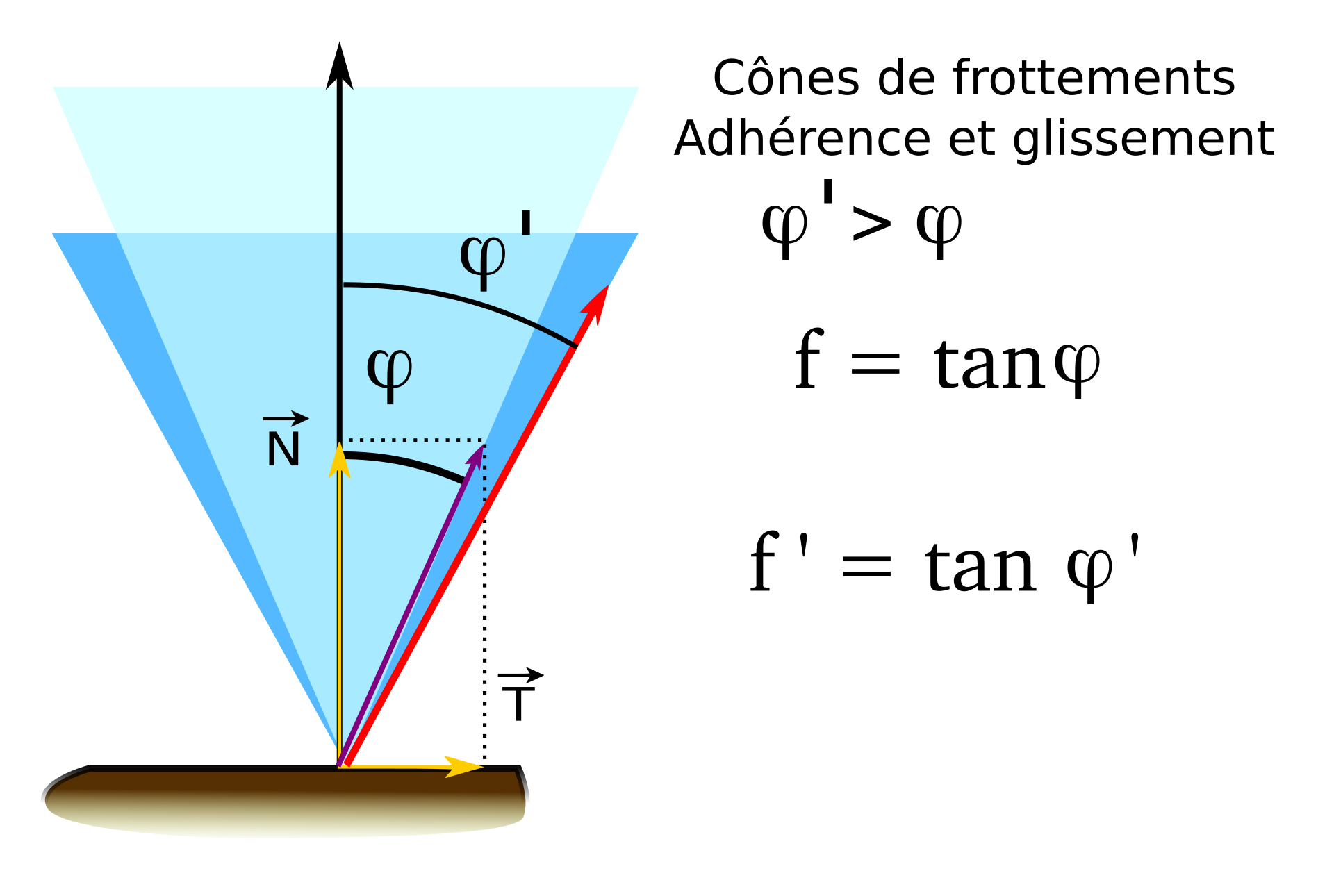
Si on considère deux corps en contact ponctuel avec frottement, il y a 2 situations à observer selon que le glissement entre les deux corps est adhéré ou pas.
- Si les corps ne glissent pas, la droite d’action transmissible peut s’écarter de la normale de contact jusqu’à une limite fixe (en rouge sur la figure). Le domaine ainsi délimité prend la forme d’un cône dit « cône de frottement d’adhérence ». Le demi angle au sommet est appelé angle d’adhérence. L'étude du cas à la frontière du cône est appelé équilibre strict.
- Si la vitesse relative entre les corps devient non nulle, alors la droite d’action prend une inclinaison fixe (violet). On définit de même le « cône de frottement de glissement ».
En général, le cône de glissement est inclus à l’intérieur du cône d’adhérence. Chacun a fait l’expérience de pousser une armoire et de s’apercevoir qu’il est moins dur d’entretenir son glissement, une fois qu’elle a décollé. C’est aussi cette différence qui explique le broutement des chaises qu’on traîne, le sifflement des freins, ou la génération du son des violons et autres instruments à archet. À une bien plus grande échelle, les séismes en sont les conséquences.
Pour certains couples de matériaux, le coefficient d'adhérence est au contraire plus faible que le coefficient de frottement, celui-ci augmentant plus ou moins notablement avec la vitesse de glissement. Ce comportement est recherché pour la conception de nombreux mécanismes industriels afin d'introduire une certaine sécurité intrinsèque et surtout de limiter les vibrations ; voir à ce sujet le wikilivre de tribologie et plus spécialement les chapitres consacrés à la modélisation des actions de contact, aux embrayages, aux freins, etc.
Lois de Coulomb
Dans les deux situations précédentes, la direction de l’action transmissible est connue :
- soit parce que le glissement est avéré ;
- soit parce que l'équilibre est avéré ; l'étude statique permet alors la détermination préalable de toutes les actions mécaniques.
Nous pouvons écrire alors une relation entre l’effort presseur (composante normale N) et l’effort de frottement (composante tangentielle T): elle doit vérifier les lois de Coulomb.
- Cas du glissement avéré :
- T = N.tan Φ = N.f où f = tan Φ. f est appelé "coefficient de frottement de glissement".
- Le sens de T est tel qu'il s'oppose au glissement.
- Cas d'équilibre avéré :
- T ⩽ N.tan Φ' = N.f' où f' = tan Φ'. f' est appelé "coefficient de frottement d’adhérence".
- si l'inégalité n'est pas vérifiée, c'est que l'hypothèse d'équilibre doit être remise en question (glissement).
- Le sens de T est normalement induit par l'étude. Dans le cas de l'équilibre strict, il est arbitrairement choisi pour s'opposer au glissement probable des deux pièces.
Formule Générale
tan Φ = T/N avec tan Φ = f
Dans de nombreux cas on pose Φ = Φ'.
Φ' étant souvent très proche de Φ.
Étude de cas
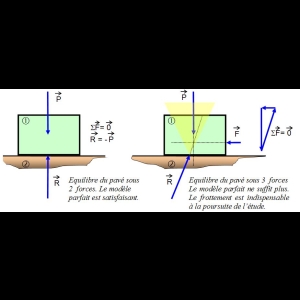
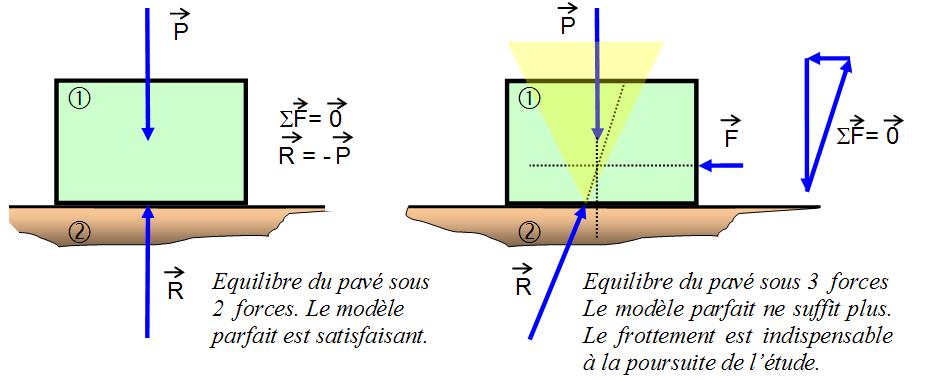
En considérant un pavé posé sur une surface plane. Si le sol est bien à niveau alors l’équilibre du pavé est possible et les forces poids P et réaction du sol R s’annulent (voir statique).
Pour déplacer ce pavé, on exerce une force latérale F. Tant que le pavé reste en place, son équilibre est toujours vrai ; ce qui impose la relation d’équilibre entre les trois forces (Principe fondamental de la statique). On remarque alors que l’action du sol n’est plus normale au contact. Il y a donc nécessairement du frottement.
Le problème reste alors entier : Peut-on connaître l’intensité de la force permettant de faire bouger le pavé, quand la seule donnée est le poids du pavé ?
On remarquera aussi que le point d'application de F modifie la position de la réaction au sol. Plus F est appliqué haut, plus l'appui au sol se fait vers l'avant. Dans le cas d'un objet très haut, une armoire par exemple, il se peut que la réaction du sol soit portée à l'extérieur (ce qui n'est pas possible, puisque cela impliquerait des actions locales de signe opposé). L'équilibre n'étant plus possible, alors il y a basculement.
Résolution de problèmes avec frottement
Dans un problème de statique, la considération du frottement ne doit pas être prise en compte si le phénomène est considéré comme négligeable. Avec un coefficient inférieur à 0,1 les droites d’action sont peu déviées (par rapport au modèle parfait), de ce fait le résultat final est peu perturbé.
Cependant le frottement doit être considéré quand on souhaite déterminer son influence sur le problème étudié, où lorsque le modèle parfait n’apporte pas de solution possible (pavé qu’on pousse mais qui cependant reste immobile). Dans ce cas 2 types d’étude sont à envisager :
1- Hypothèse de liaison avec frottement d’adhérence : l’étude est menée dans un premier temps pour déterminer l’ensemble des forces. L’hypothèse de liaison avec frottement accorde des libertés supplémentaires aux directions des droites d’action. Puis dans un deuxième temps, on vérifie que les liaisons avec frottement sont dans une situation compatible avec les lois de Coulomb (droites d’action à l’intérieur des cônes d’adhérence). Si ce n’est pas le cas, l’équilibre n’est pas possible. Il faut alors revoir la géométrie du problème.
2- Hypothèse d’équilibre strict : Quand les données sont insuffisantes, il est intéressant de poser l’hypothèse de glissement (contradictoire avec la notion d'équilibre). On fixe ainsi arbitrairement la direction de certaines actions mécaniques. Le résultat correspond alors à la situation limite au-delà de laquelle l’équilibre n’est plus possible. Cette hypothèse est aussi naturelle quand il s’agit de calculer les performances d’un système de freinage ou d’embrayage, dans ce cas les accélérations sont souvent supposées nulles ce qui élimine les considérations inertielles.
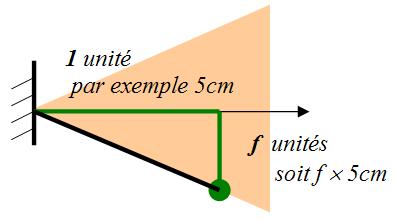
Le tracé du cône de frottement est inévitable dans les deux cas; Or la caractéristique donnée est le coefficient de frottement (tangente de l’angle). Cela est possible sans calcul en utilisant la méthode suivante (qui s’appuie sur les relations dans le triangle rectangle : tan = côté opposé / côté adjacent) :
Méthode de tracé du cône de frottement
- monter de 1 unité sur la normale de contact,
- tourner de la valeur du coefficient,
- tracer le bord du cône.
Cette méthode est plus précise que celle qui consiste à calculer l’angle puis le reporter, car les valeurs usuelles de coefficient sont voisines et les rapporteurs d’angle souvent limités en précision au demi degré.
Cas d'étude
Si un Bloc Mégalithique de 300 Tonnes est lié à des rondins de bois de chêne, qui glisse par frottement sur des rails en bois de chêne. Quelle sera la Force nécessaire pour faire avancer le traîneau?
Réponse :
f pour du Chêne sur chêne sans lubrification en Statique : 0.54
Formule : Force de traction (newton) = Poids (Kg) * G * f
300 000 * 9.81 * 0.54 = 1 589 220 Newton, soit 162 055 Kg
f pour du Chêne sur chêne avec lubrification au suif en Statique : 0.10
300 000 * 9.81 * 0.10 = 294 300 Newton, soit 30 010 Kg
Coeff. de frottement en application Mégalithique avec le Bois
Ce Coeffs. de frottement est une d'une importance capitale pour la recherche Mégalithiques, trop fort dans les 0.3 et les déplacements de Blocs deviennent quasi impossible demande beaucoup trop d'hommes pour la place possible, sans conté les cordes qui casserait. 0.04 rendrai possible les déplacements, et c'est exactement ce Coeff. que nous avons trouvé dans différentes sources à notre grande surprise, appuyé par un cas réel (Monolithe de Mussolini).
En recherchant les différents Coeffs. de frottement Bois/Bois, nous avons rencontré un premier problème, qui est la difficulté à les trouver. Une explication est qu'actuellement nous travaillons beaucoup moins avec ce matériaux, et même en formation BAC+2 ou +5 en génie mécanique le Bois n'est pas abordé.
Après recherche nous avons trouvé des valeurs dans le Guide de mécanique, montrant une forte variation du bois sous lubrification : 0.2 en statique et 0.16 à 0.04 en Dynamique. Après d'avantage de recherche nous avons trouver Arthur Morin, et retrouver les valeurs en Dynamique du Guide de mécanique dans son Tome Aide-mémoire de mécanique pratique à l'usage des officiers d'artillerie et des ingénieurs civils et militaires de 1838. Mais avec Morin nous avons 0.10 (b), 0.15 (c) en Coeffs. statique que ne reprend pas le Guide de mécanique.
Les valeurs de Morin dans son Aide-mémoire font apparaître ses valeurs sans grande justification, et qui ne sont pas mentionner dans son premier livre : Nouvelles expériences sur le frottement, faites à Metz en 1831 / par Arthur Morin,....
N'étant pas satisfait de ses valeurs jugé trop hasardeuse et trop variable, nous avons calculé le Monolithe de Mussolini afin de dégager un Coeffs. fait en Test réels.
Suite au calcul nous avons trouvé un Coeffs. surprenant et seulement lubrifié avec du Savon : 0.04 en Statique. Morin annonce 0.44 et nous trouvons 10 fois moins.
Comment expliquer cette différence? Il est probable que les Test de laboratoire ne prennent pas en conte plusieurs paramètres :
- Capacité du Bois à s'imprégner du Lubrifiant sur du long terme
- Déformation plastique du Bois permettant une meilleure imprégnation
- Déformation plastique du Bois permettant un meilleure Coeffs. de frottement
Les Tests de laboratoire étant réalisé sous faible charge, en déformation élastique, et sur du Bois neuf.
Nous retiendrons la valeur suivante pour les Coeffs. de frottement :
Statique : 0.040
Dynamique : 0.027
Le bois montre ici une grande complexité (matériaux vivant Anisotrope), et une capacité remarquable aux frottements.
Il est fort probable que de nombreuses civilisations ai remarquée cette atout du Bois et s'en soit servie pour leur transport de Blocs. La méthode "Lizzatura" est une technique millénaire qui nous démontre l'utilisation du Bois dans ses meilleures atouts de glissement.
La méthode de déplacement des Mégalithe n'a plus donc maintenant de secret, c'est la plus logique, et fonctionne en réel. A noté ses dernières années il y à beaucoup de charlatanisme autour de çà, certains Auteurs (LRDP, Leplat,...) choisissant et refusant les sources cités ici pour appuyé leur idées fumeuse. Les théories ici démontrent de façon scientifique et fiable les méthodes par glissements sur du bois par le calculs et par des cas réels.