Détails - Mégalithe
Test de Compression 1
(Comportement élastique linéaire et non-linéaire du bois en relation avec sa structure)
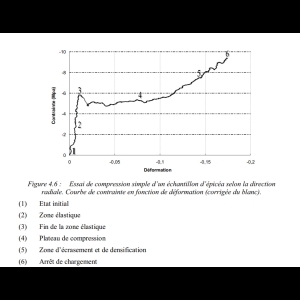
Ce Test démontre que le bois de l'épicéa peut supporté 4 Fois ou plus sa limite élastique (5Mpa) pour une déformation plastique de 60%.
Test de Compression 2
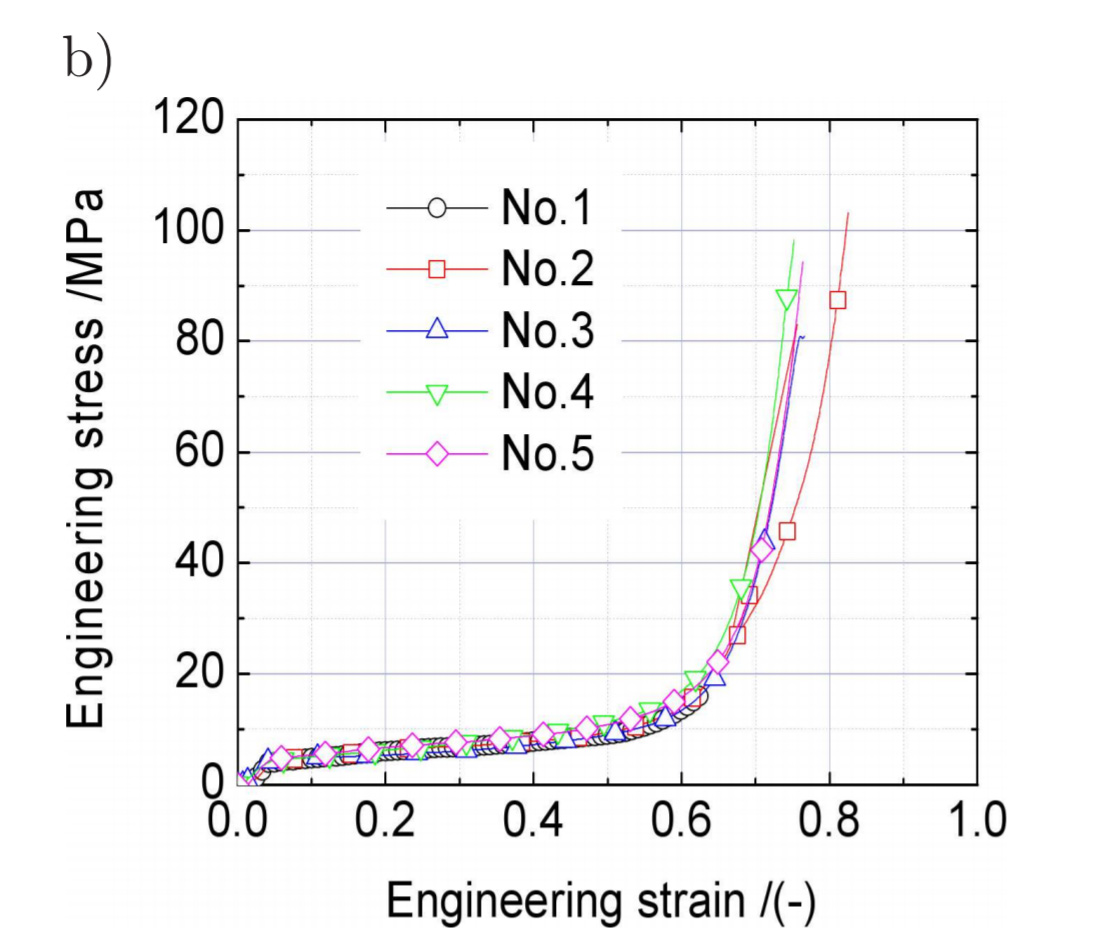
Ce Test va plus loin que le 1er en charge et démontre que les 5 échantillons de Spruce peuvent supporté 40 Mpa pour une déformation de 70%. Au dessus de 40 Mpa 3 échantillons ont subit une rupture.
On peut émettre l'hypothèse qu'un Bois en Radial peut supporté 10 fois sa limite élastique. (4Mpa pour le Spruce).
Rupture Locale : Résineux et Feuillus
Au-delà du domaine linéaire, l’anisotropie transverse reste en faveur de la direction radiale durant le plateau de compression, mais la tendance s’inverse durant le domaine de densification final. Dans ce cas, le mécanisme d’effondrement de l’agencement cellulaire et la moins bonne imbrication des parois entre-elles rend le bois plus rigide dans la direction tangentielle que dans la direction radiale. Mécaniquement, le bois de feuillus est plus « isotrope » que le bois de résineux dans le domaine de grande déformation/densification. La première rupture locale au niveau des cellules apparaît dans les deux directions, radiale et tangentielle, aux valeurs de déformation assez proches : εR=7.4% par rapport à εT=13.1%. En revanche, chez les résineux, ces valeurs de déformation sont très différentes : εR~5.1% par rapport à εT~26.1%. Chez les résineux, les ruptures locales sont apparues en mode « fragile » dans la direction radiale.
Elles apparaissent très tard mais dès leur première apparition, la structure sera détruire rapidement. En revanche, les ruptures locales sont apparues en mode « ductile » dans la direction radiale. La première apparition est très tôt mais la structure du bois reste stable dans une longue période. Chez les feuillus, les ruptures locales se font en mode « ductile » dans les deux directions, radiale et tangentielle. En outre, une observation remarquable chez les feuillus est à noter: les vaisseaux et les fibres ne sont pas cassés totalement même à la densification (ε~60%) dans toutes les deux directions. C’est le contraire chez les résineux chez qui les cellules sont complètement rompues à la même valeur de déformation.
(Source : Comportement élastique linéaire et non-linéaire du bois en relation avec sa structure)
Difficulté du Calcul Analytique en déformation plastique
Depuis les années 1970, Gillis [1972] a fait des calculs analytiques pour caractériser les propriétés élastiques du bois dans le plan transversal en utilisant la loi de Hooke et la théorie des poutres. Il a confirmé la relation entre le module élastique et le module de cisaillement dans le domaine élastique du bois, EL>ER>GLT~GLT>ET>GRT, ce qui correspond au résultat montré dans « Wood Handbook » [Anonymous, 1955 cité dans Gillis, 1972]. Au cours des dernières années, Watanabe [1999 ; 2002] et Simon [2009] ont également pris cette méthode pour calculer les propriétés mécaniques du bois des résineux en supposant que la forme de la cellule du bois soit symétrique [Watanabe, 1999 ; 2002] ou asymétrique [Simon, 2009]. Par ailleurs, d’une part, étant donné que le calcul analytique rencontre beaucoup de difficultés dans le domaine plastique en grande déformation car les cellules du bois ne gardent pas la forme initiale dans ce domaine et que les angles entre les parois cellulaires sont modifiés, il est très difficile de faire les calculs comme dans le domaine élastique. D’autre part, comme ces calculs sont basés sur des cellules modélisées identiques et uniformes, ils ne sont pas suffisants pour démontrer tenant compte de tous les détails morphologiques d’un matériau très complexe comme le bois.
(Source : Comportement élastique linéaire et non-linéaire du bois en relation avec sa structure)